Тема 5. Итерация и рекурсия

На практике часто приходится работать с последовательностями чисел. Некоторые из них вам уже знакомы. Например, самой простой последовательностью чисел является арифметиечская прогрессия.

В последовательностях обычно каждый последующий элемент выражается через предыдущий. Например, для арифметической последовательности мы можем записать такое выражение:

ai+1 = ai + b

То есть мы записали формулу как вячислить следующий (i+1-ый) элемент последовательности через предыдущий (i-ый) элемент. Такие выражения называются рекуррентными.

Приведем еще один пример: числа Фибоначчи. Первые два числа равны соответственно F0=0, F1=1, а все последующие получаются в результате сложения двух предыдущих. В этом случае рекуррентная формула будет иметь вид:

Fi = Fi-1 + Fi-2

Если в случае арифметической прогрессией расчитать любой элемент достаточно просто: ai+1 = a0 + b×i

Для того чтобы вычислить некоторый элемент в соответствии с рекуррентной формулой можно воспользоваться двумя вариантами организации кода: итеративный расчет и рекурсия.

В случае итеративного расчета вычисления организуются в цикле с заданным числом повторов (итераций) в соответствии с рекуррентной формулой. Для организации итеративного расчета следует задать начальное значение, конечное значение, а также реализовать рекуррентную формулу в виде кода:

Рекурсивная функция это такая функция, которая вызывает сама себя. При этом в любой рекурсивной функции помимо вызова самой себя должно быть условие завершения цикла рекурсии.

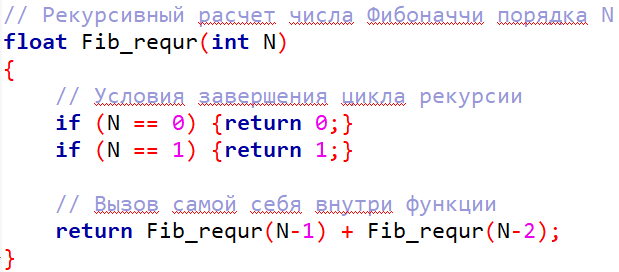
Таким образом, рекурсивные функции часто получаются весьма компактными, но при этом такая реализация может оказаться достаточно требовательной к ресурсам компьютера.